Optimal Trajectory

Back to Index    Next Example

Find the optimal angle for which the nonlinear trajectory reaches a given target. While an elementary physics problem at heart, the solution nicely illustrates the evolution from a simple simulation to an adaptive pursuit of a set objective. Trajectory equations of motion are governed by,

        mx" + Dcos(alfa) = 0
	my" + Dsin(alfa) + mg = 0

where an atmospheric drag force and angle of attack are defined as,

        D = .5*Cd*A*rho(h)*v^2
	alfa = atan(vy/vx)

Let's examine the possibilities with a quick pseudo-code, setting up the blueprint for screening the solution strategies...

<INIT>   Initialize equations of motion

               do while ( height  >  0 )
                  integrate (eom)
               end do

               if ( obj_fcn  >  criteria ) then
                  optimize (alfa)
                  go to  <INIT>
               end if

Quite ordinary at first glance until attempting to solve for a specific trajectory raises the question of how to coordinate the integrate and optimize modules to arrive at the solution. The "seamless" graphical environments suddenly fade into the sunset and reality sets in... you've been had!

Problems requiring collaborative manipulation of solution methods quickly draw out the deficiencies which marketers of various simulation wares are trying hard to obscure. Some of the most glaring:

• Most real-world problems do not fit a tidy graphical modeling scheme.
• Built-in philosophy that simulation is solely an IVP solver is long overdue for overhaul.
• Lack of control over the mode of operation which is essential to computer aided engineering.
• Script-type proprietary "dialects" are a poor substitute for standardized languages.

The SDX solution clearly exhibits the absence of any such shortcomings. To underscore this point we searched unsuccessfully for alternate software solutions which are summed up in the competitors' corner.

Search for optimal trajectory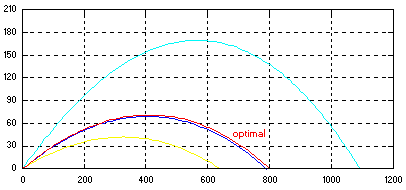

Note shadow trajectories due to evaluation of local Jacobian are invisible.
i.e. actual trajectory count is double.

Trajectory determination code

      call optimal (iopt,isim,m,n,alfa,range,tol,pif)
      if(isim .eq. 1) call oprtn                 ! start simulation

      if(mode() .eq. initialize) then                     
        dist   = 0
        height = 0
        vx     = v0*cos(alfa)
        vy     = v0*sin(alfa)
      endif

*        Define & integrate eom
      vsq  =  vx**2 + vy**2
      Drag = .5*Cd*Ap*rho(height)*vsq
      alfa =  atan(vy/vx)

      dx(1) =  vx
      dx(2) = -(Drag/mass)*cos(alfa)
      dx(3) =  vy
      dx(4) = -(Drag/mass)*sin(alfa) - g

      call integral (mode(),dt(),4,S,id,dmy,dmy,x,dx)
*
      if(height .lt. 0.) then                    ! reset on impact
        isim = 0
        call icrtn
        xhit = dist - height*vx/vy
        pif  = abs(xhit - target)
      endif

Competitors' corner -- It would be a useful comparison to present solutions applying different tools to the same problem. However, both principal vendors failed to come up with one, in contrast to their marketing claims of quick and easy solutions.