Previous Example    Next Example

Generate a numerical solution to a dynamic system,

                iAz' = Sz

where A and S are n by n complex valued matrices. The complex nature elevates this problem from the ordinary yet it is easy to solve given the right set of tools. First, rewrite the system as,

		z' = -iA^(-1)Sz = Cz

Expanding the complex elements and some algebra yields a system of coupled differential equations,

		zr' = Cr*zr - Ci*zi
		zi' = Ci*zr + Cr*zi

which completes the preparation. The complex algebra was left intact so that netlib can be utilized to evaluate matrix C. Mapping the real and imaginary parts of C into diagonal blocks of the composite system matrix sets the stage for state propagation by a rate driven recursion,

		x(k+1) =  x(k) + Px'(k)

where P is a generalized transition matrix. The complex solution trajectories are then reassembled from the components of the state vector.

As indicated, the objective was to demonstrate the role SDX open environment has in the development process. In fact, a few quick downloads is often all it takes to craft a custom solution model.

Simulation Model

*        Calculate composite matrix R
      if(init() .eq. 1) then
        call minv (n,A)
        call mmul (n,A,S,C)
        call mmap (n,C,R)
      endif

*        Solve d/dt x = R*x
      call xdot (2*n,R,x,dx)
      call propagate (mode(),dt(),2*n,R,id,dmu,dmy,x,dx)

*        Construct solution to d/dt z = C*z
      do  j=1,n
        z(j) = cmplx (x(j),x(n+j))
      enddo

Notes:   minv and mmul encapsulate LAPACK's (cgetrf, cgetri, cgemm) factorization, inverse and matrix multiply routines. Aside the model, mmap and xdot are the only code written for this application. Though short, they are not in-lined in order to keep the algorithm flow fully transparent.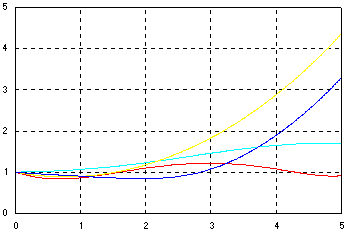

Simulation Output

Norms of the complex trajectories ||z|| vs. time
for a four dimensional dynamic system.